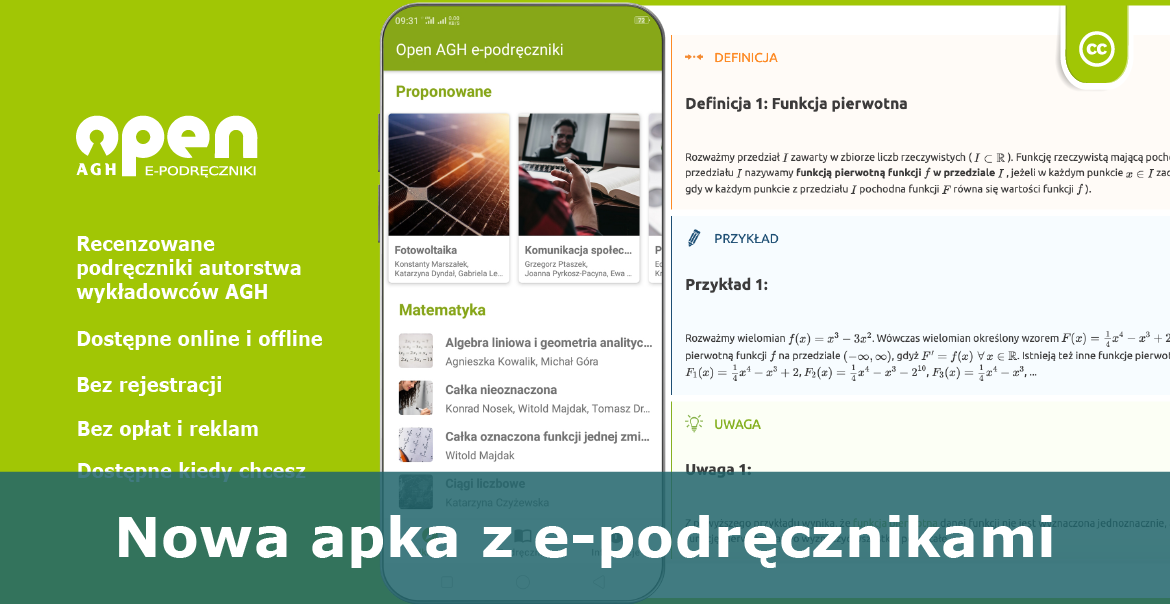
Najlepiej oceniane zasoby

Nasz serwis to ponad 1000 godzin nauki

Z naszych zasobów miesięcznie korzysta ponad 4500 osób

Dzięki naszym zasobom zdanych zostało 921547 egzaminów :-)
4 Zasoby
4 Zasoby
14 Zasobów
16 Zasobów
2 Zasoby
6 Zasobów
3 Zasoby
1 Zasób